Parametric Curves

Curves and surfaces can have explicit, implicit, and parametric representations. Parametric representations are the most common in computer graphics.

Reparameterization

Parameterizations are in general not unique. Consider the following parameterizations for a line:
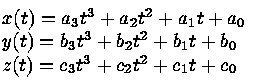
  L(P0,P1) = P0 + u(P1-P0),  u = [0...1]
  L(P0,P1) = v(P1-P0)/2 + (P1+P0)/2,  v = [-1...1]
Parameterizations can be changed to lie between desired bounds. To reparameterize from u = [a...b] to w = [0...1], we can use w = (u-a)/(b-a), which gives u = w(b-a) + a. Thus, we have: 
  P(u), u = [a...b]   =    P(w(b-a)+a), w = [0...1]

Parametric Cubic Curves

Cubic curves are commonly used in graphics because curves of lower order commonly have too little flexibility, while curves of higher order are usually considered unnecessarily complex and make it easy to introduce undesired wiggles.

A parametric cubic curve in 3D is defined by:

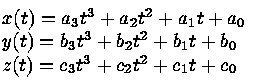
Usually, we consider t = [0...1].


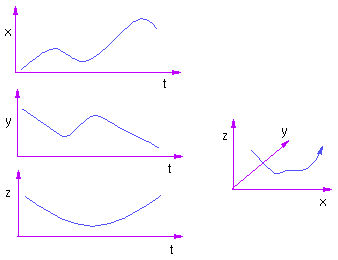
A compact version of the parametric equations can be written as follows:

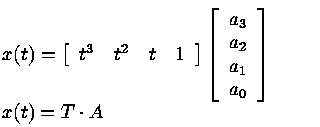
Similarly, we can write 

  y(t) = T B
  z(t) = T C
Each dimension is treated independently, so we can deal with curves in any number of dimensions.

The derivatives of the curve with respect to t can be expressed as follows: 

  x'(t) = [3t^2  2t  1  0] A
It is often convenient to think of the parameter t as being time in order to visualize some of the properties of the curve. The derivatives also have an intuitive interpretation in the cartesian space of the curve:

A First Example

Suppose we wish to define a cubic curve such that the user specifies the position of two endpoints and a midpoint, as well as the tangent at the midpoint. The following figure illustrates some sample curves.


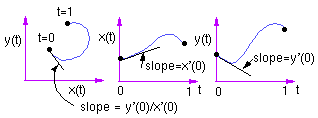
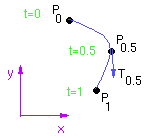
We'll first construct the cubic curve for x(t). There are four constraints that are to be met and four unknowns:



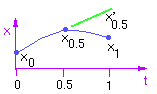
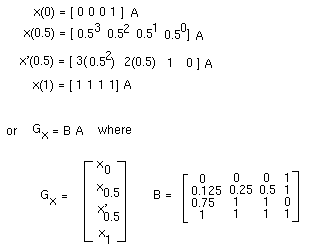
We can solve for A using A = B_inv G_x. The final equation for x is thus: 

  x(t) = T B_inv G_x
The matrix B_inv is often called the basis matrix, which we shall denote by M. We can thus write 
  x(t) = T M G_x
In this case, we have 
      [ -4  0 -4  4 ]
  M = [  8 -4  6 -4 ]
      [ -5  4 -2  1 ]
      [  1  0  0  0 ]
Lastly, we can also write 
  x(t) = [ f1(t) f2(t) f3(t) f4(t) ] G_x
where f1(t) ... f4(t) are the functions obtained from the product T M. These are functions are called the blending or basis functions, because they serve to give a weighting to the various components of the geometry vector, G. In this case, these are 
f1(t) = -4t^3 + 8t^2 - 5t + 1
f2(t) = -4t^2 + 4t
f3(t) = -4t^3 + 6t^2 - 2t
f4(t) =  4t^3 - 4t^2 + 1,
where f1(t) is the weighting function for P0, f2(t) is the weighting function for P0.5, f3(t) is the weighting function for T0.5, and f4(t) is the weighting function for P1. These basis functions look as follows:

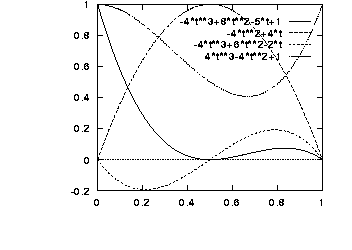
The curves for y(t) and z(t) are contructed in an analogous fashion to that for x(t). The basis matrix and basis functions thus remain the same. Only the geometry vector changes. The geometry vector for y(t) gives the y components of P0, P0.5, T0.5, and P1. In general, we can write the curve as a single vector equation 
P(t) = T M G
which encompasses the following three equations: 
x(t) = T M G_x
y(t) = T M G_y
z(t) = T M G_z

Hermite Curves

As a second example, let's look at Hermite curves. Hermite curves are defined by two points and two tangent vectors.


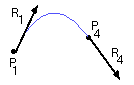
Let's derive the equation for Hermite curves using the following geometry vector: 

G_h = [ P1 P4 R1 R4 ]^T
As before, we'll express the curve as: 
x(t) = T A_h
     = T M_h G_h
The constraints we'll use to define the curve are: 
x(0)  = P1 = [ 0 0 0 1 ] A_h
x(1)  = P4 = [ 1 1 1 1 ] A_h
x'(0) = R1 = [ 0 0 1 0 ] A_h
x'(1) = R4 = [ 3 2 1 0 ] A_h
Writing these constraints in matrix form gives: 
G_h = B_h A_h
A_h = inv(B_h) G_h
x(t) = T A_h
     = T inv(B_h) G_h
     = T M_h  G_h
The inverse of B_h is thus defined as the basis matrix for the hermite curve. 
      [  2 -2  1  1 ]
M_h = [ -3  3 -2 -1 ]
      [  0  0  1  0 ]
      [  1  0  0  0 ]
As before, the basis functions are the weighting factors for the terms in the geometry vector, and are given by the product T M_h. Thus, for basis functions for Hermite curves are 
f1(t) =  2t^3 - 3t^2 + 1
f2(t) = -2t^3 + 3t^2
f3(t) =   t^3 - 2t^2 + t
f4(t) =   t^3 -  t^2
These basis functions look as follows:

Bezier Curves

Bezier curves are a variation of the Hermite curves. They are specified by four points:

The curve is closely related to the Hermite curve: 
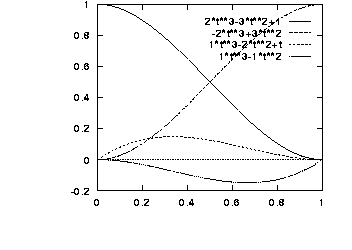
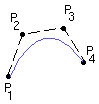
P1_h = P1
P4_h = P4
R1_h = 3 (P2 - P1)
R4_h = 3 (P4 - P3)
We'll arrive at the basis matrix by expressing the above in matrix form: 
[ P1_h ]   [  1 0  0 0 ] [ P1 ]
[ P4_h ] = [  0 0  0 1 ] [ P2 ]
[ R1_h ]   [ -3 3  0 0 ] [ P3 ]
[ R4_h ]   [  0 0 -3 3 ] [ P4 ]

P_h = M_bh P_b
The equation for a bezier curve can thus be written as: 
P(t) = T M_h M_bh P_b
P(t) = T M_b P_b
where 
      [ -1  3 -3  1 ]
M_b = [  3 -6  3  0 ]
      [ -3  3  0  0 ]
      [  1  0  0  0 ]

The Bezier basis functions are as follows: 
P(t) = T M_b G_b
     = f1(t) P1 + f2(t) P2 + f3(t) P3 + f4(t) P4
where
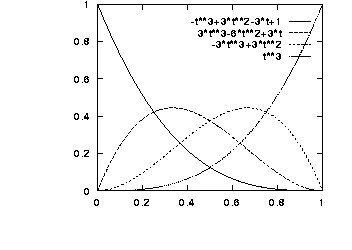
  f1(t) =  -t^3 + 3t^2 - 3t + 1
  f2(t) =  3t^3 - 6t^2 + 3t
  f3(t) = -3t^3 + 3t^2
  f4(t) = t^3

or alternatively, 

  f1(t) = (1-t)^3
  f2(t) = 3t (1-t)^2
  f3(t) = 3t^2 (1-t)
  f4(t) = t^3


Convex hull property
The convex hull property ensures that the curve will never pass outside of the convex hull formed by the four control vertices. As such, it lends a measure of predictability to the curve. The Bezier basis functions satisfy the conditions necessary for the convex hull property, namely:

Bezier Curves of degree n

It is not per chance that the basis functions for Bezier curves have the convex hull property. How might one then go about designing a set of basis functions that sum to one and ensure that each individual basis function remain in the range [0,1]? The Bernstein polynomials have exactly the required properties.

Using the Bernsteinn polynomials, we can construct a Bezier curve of arbitrary degree. For curves of higher degree than the cubic Bezier curve discussed thus far, we'll need more than four control points. The general Bezier curve of degree n is given by

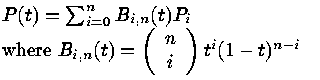
The basis functions are equivalent to the terms arising from the expansion of

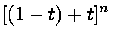
using the binomial expansion theorem. It is also obvious from this why the sum of all the terms is equal to one.

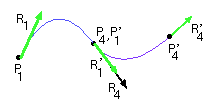
Piecewise Hermite and Bezier Curves

Hermite curve segments can be connected in a continuous fashion by ensuring that the end-point of one curve is the same as the starting point of another, as well as ensuring that the tangent vectors for this point have the same direction.


In terms of the above figure, this means P1'=P4, R1'=k R4 . For a Bezier curve, the conditions are that the the last two points of one curve and the first two points of the second curve are aligned.

Geometric and Parametric Continuity

Geometric Continuity Parametric Continuity As their names imply, geometric continuity requires the geometry to be continuous, while parametric continuity requires that the underlying parameterization be continuous as well.

Parametric continuity of order n implies geometric continuity of order n, but not vice-versa.

Summary of Bezier and Hermite Curves

Splines

The following is an example of a five-segment B-spline curve (although this is simply a hand-drawn example). The points which indicate the ends of the individual curve segments and thus the join points are known as the knots.


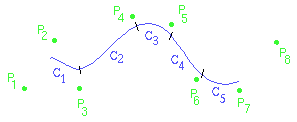
Each curve segment is determined by four control points, as follows:


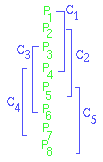
B-spline curves are defined by a basis matrix, just like the other types of cubic curves. We shall not discuss the derivation of this matrix here. 

                [ -1  3 -3 1 ]
M_bspline = 1/6 [  3 -6  3 0 ]
                [ -3  0  3 0 ]
                [  1  4  1 0 ]
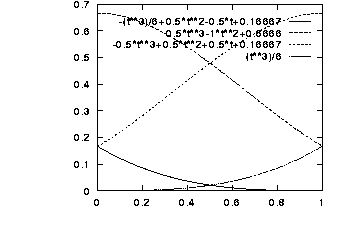
where the geometry vector consists of four consecutive control points. It is easy to show that B-spline curves are C2 continuous and that they satisfy the convex-hull property. The basis functions for B-splines are as follows:


Multiple knots
Control vertices can be repeated in order to allow for reduced geometric continuity at the join points.

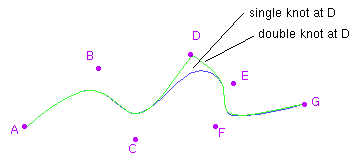
multiplicity
1 G2 continuous
2 G1 continuous
3 G0 continuous, interpolates point


NURBS: Nonuniform Rational B-splines

One of the disadvantages of the curves discussed to date is that they cannot be used to create common conic shapes such as circles, ellipses, parabolas, etc. This can be done using rational cubic curves, however. A rational cubic curve segment in 3D can be constructed as follows 
  x(t) = X(t)/W(t)
  y(t) = Y(t)/W(t)
  z(t) = Z(t)/W(t)
where each of X(t), Y(t), Z(t), and W(t) are cubic polynomial curves. Defining curves as rational polynomials in this manner allows for simple exact represenations of conic sections such as circles, as well as curves which are invariant under perspective projection.
From University of Toronto -- See deatails