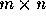matrix. It is represented as
It may be thought of as an ordered set of vectors.
Let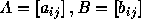 
be two matrices. Matrices A and B are said to be
equal if they are of the same order, i.e. have the same number of rows and and the same number of coloumns, and
.
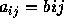For any matrix, if the number of rows
is equal to that of the coloumns, then that matrix is called
the square matrix.
Addition of two matrices A and B is possible only if
the two matrices are equal.
The resultant matrix C is obtained by adding the
corresponding elements. It is also
of the same order as that of A and B i.e.
. For example,
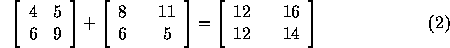
Matrix addition is commutative i.e. A+B = B+A.
It is also associative i.e.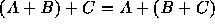 
.
Subtraction of two matrices A and B is analogous to
matrix addition. The two matrices should be equal;
the operation is performed elementwise i.e.
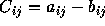. For example
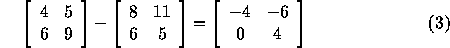
Multiplying scalar times a matrix is similar to matrix addition or subtraction. For example,
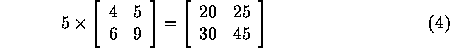
Matrix multiplication is slightly different from what we have seen before.
Let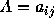 
and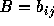 
be two matrices of order 
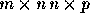respectively. The product of these two matrices C=A B is defined only
if the number of coloumns of A equals number of rows of
B.
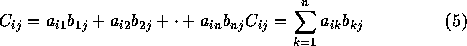
The resultant matrix will have as many rows as A
and as many coloumns as B. Thus C will be of order
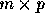. For example,
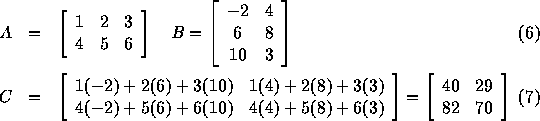
It can be noted that matrix multiplication is not commutative
i.e.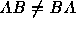 
. It is interesting to note that
matrix multiplication is the inner product
of the two matrices.
The transpose of matrix A, denoted by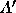 
is
obtained by changing all the rows of A into
coloumns of 
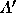, while preserving the order.
Let matrix A be
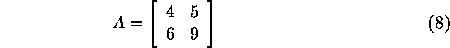
Then its transpose is given by
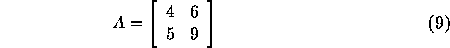
The transpose of the transpose matrix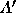 
is the original matrix A, i.e. 
.
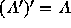From P. Asokarathinam -- see details 27.11.1996