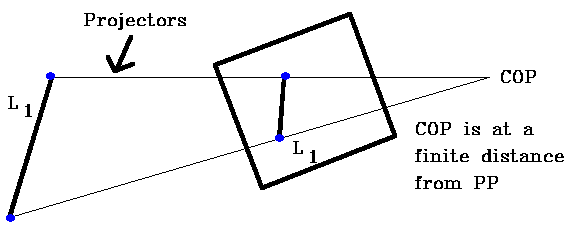
The Perspective viewing projection has a Center of Projection ("eye") at a finite distance from the projection plane (PP).

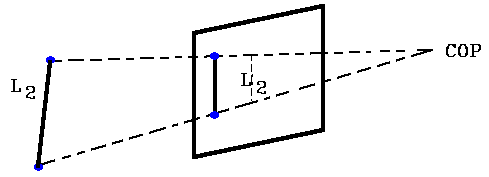
So the distance of a line from the projection plane determines its size on the projection plane, i.e. the farther the line is from the projection plane, the smaller its image on the projection plane. In the two images above, the projections of L1 = L2 but the actual length of L1 <> L2. Perspective projection is more realistic since distant objects appear smaller.
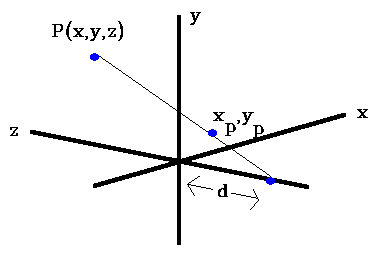
Look at above diagram from y axis
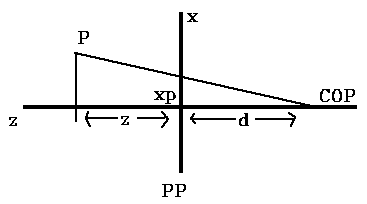
Now x / (z+d) = xp/d
xp = x[d / (z+d)]
xp = x / (z / d + 1)
Do same for y (look down the x axis) and get
y p = y / (z / d+1)
zp = 0
Note that we can increase the perspective effect by decreasing d (moving closer). We can represent this in matrix form by using homogeneuos coordinates as follows:
[xh yh zh w]=[x y z 1] |1 0 0 0 | |0 1 0 0 | |0 0 01/d| |0 0 0 1 |
where:
xh = x
yh= y
zh = 0
w = (z/d) + 1
And Points on the projection plane are [xp yp zp 1] = [xh/w yh/w zh/w 1]
This leads to the same xp, yp as before.
A problem with a perspective transformation is that it does not preserve straight lines or planes, i.e., straight lines are not transformed into straight lines and planes are no longer planar after the transformation.
Look at example of a 3D line in object space from:
P1 (x1 = 2.0, y1 = 5.0, z1 = 6.0) to P2 (x2 = 8.0, y2 = 7.0, z2 = 12.0)
In parametric form this line is represented as:
x(t) = 2 + 6 × t
y(t) = 5 + 2 × t
z(t) = 6 + 6 × t
Let us choose an arbitrary value of t (t = 0.4) and compute the x, y, z values)
x = 2 + 2 × 0.4 = 4.4
y = 5 + 2 × 0.4 = 5.8 so Pi(t = 0.4) = (4.4, 5.8, 8.4)
z = 6 + 6 × 0.4 = 8.4
Now perform the perspective transformation (assume d = 10.0) for P1, Pi, P2. Then we get for the transformed points:
P1(x = 1.25, y = 3.125, z = 6); Pi(x = 2.39, y = 3.15, z = 8.4);
P2(x = 3.64, y = 3.18, z = 12)
If this is still a straight line then all three coordinates of point Pi must have the same value of the parameter t.
so for x we get 2.39 = 1.25 + t × (2.39) =>t = 0.48
for y we get 3.15 = 3.12 + t × (0.57) => t = 0.48
for z we get t = 0.40 since unchanged => therefore the points are not collinear.
To maintain linearity we can do a perspective depth transformation:
Zp = Z / (D + Z)
Then for point 1 Zp = 6 / (10+6) = .375
point 2 Zp = 12 / (10+12) = .545
point i Zp = 8.4 / (10+8.4) = .457
Now check with t value for point i 0.457 = 0.375 + t * (0.170) = .48. This is the same t value we got for point i x and y. Therefore points 1, 2, and i are still colinear after the perspective depth transformation.. Note that the relative z depth values remain unchanged, i.e. if Z1 < Z2 then Z1 / (Z1+d) < Z2 / (Z2+d) as shown below:
Z1 < Z2
Z1 × d < Z2 × d multiply both sides by d
(Z1 × Z2 + Z1 × d) < (Z1 × Z2 + Z2 × d) add Z1 × Z2 to both sides
Z1 × (Z2 + d) < Z2 × (Z1 + d)
Z1 / (Z1 + d) < Z2 / (Z2 + d)
Note that for Zp = Z / (Z+d) => 0 if d >> Z and => 1.0 if Z >> d
therefore 0.0 <= Zp <= 1.0
So to maintain linearity (or planarity) we must transform Z as well as X and Y.
From HyperGraph -- see details 27.11.1996