Projection rays (projectors) emanate from a Center of Projection (COP) and intersect Projection Plane (PP). The COP for parallel projectors is at infinity. The length of a line on the projection plane is the same as the "true Length".

There are two different types of parallel projections:
If the direction of projection is perpendicular to the projection plane then it is an orthographic
projection. If the direction of projection is not perpendicular to the projection plane then it is an
oblique projection.
Look at the parallel projection of a point (x, y, z). (Note the left handed coordinate system). The projection plane is at z = 0. x, y are the orthographic projection values and xp, yp are the oblique projection values (at angle a with the projection plane)
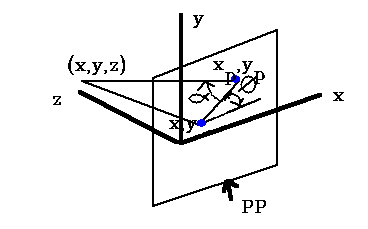
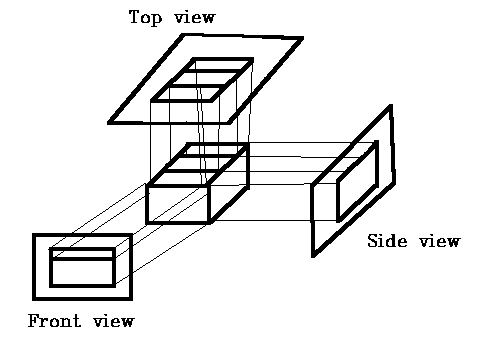
Look at orthographic projection: it is simple, just discard the z coordinates. Engineering drawings frequently use front, side, top orthographic views of an object.
Here are three orthographic views of an object.
Orthographic projections that show more than 1 side of an object are called axonometric orthographic projections. The most common axonometric projection is an isometric projection where the projection plane intersects each coordinate axis in the model coordinate system at an equal distance.
Isometric Projection
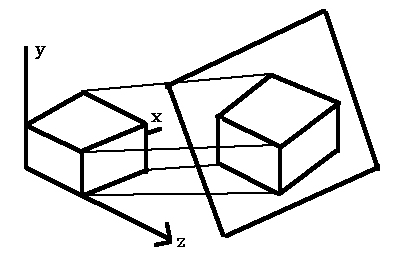
The projection plane intersects the x, y, z axes at equal distances and the projection plane Normal makes an equal angle with the three axes.
To form an orthographic projection xp = x, yp= y , zp = 0. To form different types e.g., Isometric, just manipulate object with 3D transformations.
Oblique Projection

The projectors are not perpendicular to the projection plane but are parallel from the object to
the projection plane The projectors are defined by two angles A and d where:
A = angle of line (x,y,xp,yp) with projection plane,
d = angle of line (x, y, xp, yp) with x axis in projection plane
L = Length of Line (x,y,xp,yp).
Then:
cos d = (xp - x) / L ------> xp = x + Lcos d ,
sin d = (yp - y) / L ------> yp = y + Lsin d ,
tan A = z / L
Now define L1 = L / z ----> L= L1 z , so tan A = z / L = 1 / L1 ; xp = x + z(L1cos d) ; yp = y + z(L1sin d)
|1 0 0 0 |
P = |0 1 0 0 |
|L1cosq L1sinq 1 0 |
|0 0 0 1 |
Now if A = 90° (projection line is perpendicular to PP) then tanA = infinity => L1 = 0, so have an rthographic projection.
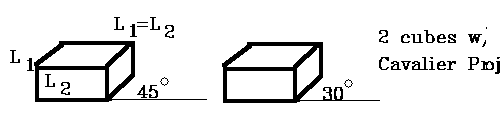
Two special cases of oblique projection
A) A = 45° , tanA = 1 => L1 = 1 This is a Cavalier projection such that all lines
perpendicular to the projection planeare projected with no change in length.
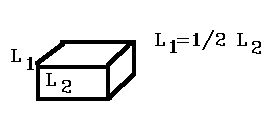
B) tanA = 2, A= 63.40°, L1 = 1 / 2
Lines which are perpendicular to the projection planeare projected at 1 / 2 length . This is a
Cabinet projection.
From HyperGraph -- see details 27.11.1996