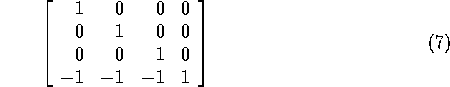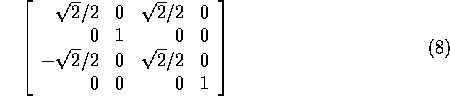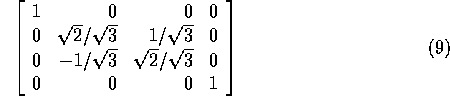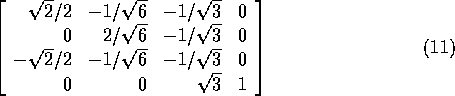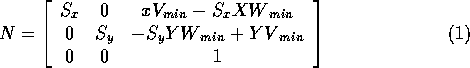
Viewing Transformation is the mapping of coordinates of points and lines that form the picture into appropriate coordinates on the display device.
World coordinate system (WCS) is the right handed cartesian co-ordinate system where we define the picture to be displayed. A finite region in the WCS is called the Window. The corresponding coordinate system on the display device where the image of the picture is displayed is called the physical coordinate system. Mapping the window onto a subregion of the display device called the viewport is called the Viewing Transformation. Normalized device coordinate (NDC) is the display area of the virtual display device corresponding to a unit square. The lower left handed corner is the origin of the coordinate system. Mapping the window in the world coordinate space to viewport in NDC space is called the Normalization Transformation, N.
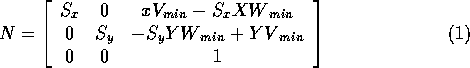
where 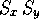 is the scale in x and y directions, given by
is the scale in x and y directions, given by
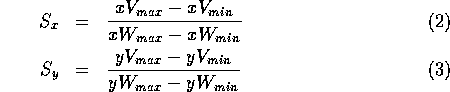
A 3D scene can be viewed from any posistion in 3D space. A "synthetic" camera positioned and oriented in 3D space can be used to describe the viewing, and the part of the image or scene to be viewed . It has the following three principal ingredients.
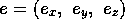 .
.
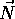 .
.
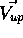 is a unit vector perpendicular to
is a unit vector perpendicular to
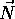 .
.
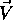 , the y-axis of the view coordinate system
is the perpendicular projection of
, the y-axis of the view coordinate system
is the perpendicular projection of
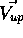 on the view plane.
on the view plane.
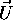 , the x-axis of the view coordinates, is
orthogonal to
, the x-axis of the view coordinates, is
orthogonal to 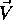 and
and 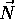 i.e.
i.e.

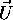 and
and 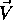 are to the right
and up-direction from eye's point of view.
are to the right
and up-direction from eye's point of view.
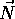 is the z-axis of the view coordinate.
It increases in positive direction with depth of a point
from the eye.
is the z-axis of the view coordinate.
It increases in positive direction with depth of a point
from the eye.
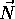 and e determines a plane orthogonal to
and e determines a plane orthogonal to 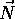 containing e.
containing e.
Let 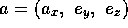 be the look-at-point.
For perspective views, the view plane normal as a unit vector from eye to a ``look-at point'' is given by
be the look-at-point.
For perspective views, the view plane normal as a unit vector from eye to a ``look-at point'' is given by
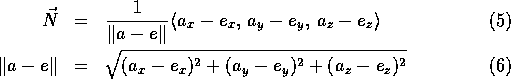
The view up vector is the tilt (rotation) of the head or camera.
For parallel views it is convenient to think of the view plane normal as determining the direction of projection.
An object in world coordinate space, whose vertices
are 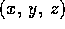 can be expressed in term of
view coordinates
can be expressed in term of
view coordinates 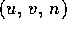 .
.
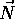 axis into the yz plane of world coordinates
axis into the yz plane of world coordinates
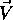 axis with the y
axis with the y
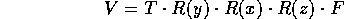
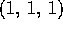 be the view reference point.
be the view reference point.
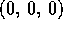 be the look-at point.
be the look-at point.
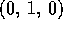 be the up vector.
be the up vector.