Knuth-Morris-Pratt-algoritmi

Kuva 1: KMP-jononsovitusautomaatti $Q$, kun $P = aikalainen$

Hahmontunnistus voidaan suorittaa $O(m+n)$ ajassa yksinkertaista äärellistä automaattia käyttävällä algoritmilla. Ideana on, että tekstissä ei siirrytä koskaan taaksepäin. Tähän päästään huomaamalla, että jos $s_i \ne p_j$, tiedetään kuitenkin, että $s_{i-j+1}=p_1, s_{i-j+2}=p_2, ..., s_{i-1}=p_{j-1}$. Oletetaan, että meillä on käytössä jonon $P_j=p_1p_2...p_{j-1}$ (jono, jonka tiedetään täsmäävän) pisimmän alkuosan pituus $k_j$. Tämä pisin alkuosa on myös jonon $P_j$ loppuosa. Toisin sanoen $p_1p_2...p_{k-1}=p_{j-k-1}p_{j-k}p_{j-k+1}...p_{j-1}$ ja $p_1p_2...p_{k-1} p_k...p_{j-k} p_1...p_{k-1} = P_j$. Vertailua voidaan nyt jatkaa kokeilemalla, onko $s_i=p_{k+1}$, koska $s_i$:n vasemmalla puolella tiedetään olevan $k$ täsmäystä.

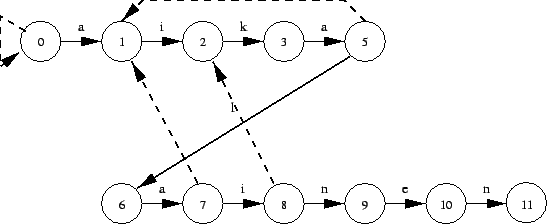
Algoritmin toteutuksessa muodostetaan aluksi $m+1$-tilainen äärellinen automaatti $Q$ (kuva 1), joka sisältää tilat $\{q_1, q_2, ... , q_{m+1}\}$. Automaatin alkutila on $q_1$ ja lopputila $q_{m+1}$. Automaatissa on jokaisella hahmon merkillä $p_j$ tilasiirtymä tilasta $q_j$ tilaan $q_{j+1}$. Lisäksi jokaisesta tilasta $q_j$ on korjaussiirtymä tilaan $q_{k_j+1}$. Algoritmi suoritetaan selaamalla tekstiä merkki $s_i$ kerrallaan seuraavasti:

• Täsmäävät merkit aiheuttavat tilasiirtymän tilasta $q_j$ tilaan $q_{j+1}$. Tekstissä edetään seuraavaan merkkiin $s_{i+1}$.
• Epätäsmäys aiheuttaa korjaussiirtymän tilasta $q_j$ tilaan $q_{k_j+1}$. Tekstissä ei edetä.
• Lopputilaan saapuminen merkitsee hahmon löytymistä tekstin positiosta $i-m$.
• Mikäli merkki ei täsmännyt korjaussiirtymienkään jälkeen, siirrytään tekstissä seuraavaan merkkiin $s_{i+1}$.

Käytännön toteutuksessa ei muodosteta varsinaista automaattia, vaan käytetään indeksimuuttujaa $j$, joka vastaa automaatin $Q$ tilaa $q_j$. Lisäksi käytössä on taulukko $fail$, jonka alkio $fail[j]$ sisältää uuden arvon $j$:lle (korjaussiirtymän jälkeisen tilan numeron), mikäli $p_j \not= p_i$.

Automaatin $Q$ muodostamisen aikavaatimus on $O(m)$. Tekstin selaamisen aikavaatimus taas on $O(n)$. Näin ollen KMP-algoritmin kokonaisaikavaatimus on $O(m+n)$.