On-line algoritmi loppuosapuun muodostamiseen

Kuva 4: Normaalin loppuosapuun $Trie(mamma)$ muodostaminen on-line algoritmilla

Merkitään $i$:n pituista tekstin $S$ alkuosaa $S^i$:llä. Muodostetaan ensin loppuosapuu $Trie(S^1)$. Loppuosapuu $Trie(S^{i-1})$ muunnetaan loppuosapuuksi $Trie(S^i)$. Näin $\vert S\vert-1$ muunnoksen jälkeen on loppuosapuu $Trie(S)$ muodostettu. On-line algoritmi loppuosapuun $Trie(S)$ muodostamiseen tarjoaa menetelmän kyseisen muunnoksen tekemiseen, kun merkki $s_i$ on tunnettu. Loppuosapuu siis muodostetaan viittaamalla kuhunkin tekstin $S$ merkkiin vain kerran.

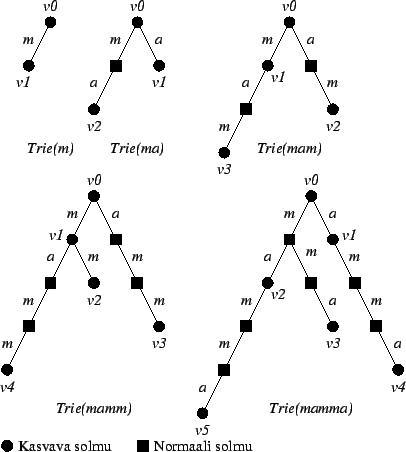
Olkoon $v_k$ kulloinkin käsiteltävänä olevan alkuosan $S^i$:n $k$:n mittainen alkuosa. Samaistetaan alkuosa $v_k$ loppuosapuun $S^i$ alkuosaa $v_k$ vastaavan polun viimeisen solmun kanssa (kuva 4). Solmut $V=v_k, v_{k-1}, ..., v_0$ ovat tällöin puun $S^i$ kasvavia solmuja (kirjan [CR94] essential nodes); ainoastaan solmuihin $V$ lisätään uusia solmuja puuta $Trie(S^i)$ muodostettaessa. Algoritmissa alkuosat $V$ säilytetään listassa alkuosien pituuden mukaan laskevassa järjestyksessä.

Olkoon $v_j$ ensimmäinen solmu listassa $V$, jolla on lapsisolmu merkillä $s_i$. Tällöin puu $Trie(S^i)$ voidaan muodostaa lisäämällä jokaiselle solmulle $v_{i-1}, v_{i-2}, ...,v_{j-1}$ lapsisolmu merkillä $s_i$. Ellei solmua $v_j$ löytynyt, lisätään lapsisolmu merkillä $s_i$ jokaiselle solmulle listassa $V$. Uusien lapsisolmujen lisäämisen yhteydessä muodostetaan uusi lista $V$ algoritmin iteraatiota $i+1$ varten.

Listan $V$ toteutus on oleellinen algoritmin tehokkuuden kannalta. Mikäli $V$ toteutetaan listana, joka luodaan uudelleen algoritmin jokaisessa iteraatiossa, on algoritmin aikavaatimus parhaassakin tapauksessa kaikkien luotujen listojen $V$ pituuksien summa $\Sigma_{i=1}^{\vert S\vert}\vert V_i\vert=\Sigma_{i=1}^{\vert S\vert}i={1 \over 2}\vert S\vert^2$ eli neliöllinen. Lista $V$ voidaan kuitenkin toteuttaa lisäämällä jokaiseen puun solmuun, johon tullaan merkillä $c$, linkki puussa seuraavaksi juurta lähempänä olevalla tasolla olevaan solmuun, johon päästään merkillä $c$, tai joka on juurisolmu. Tällöin uuden listan $V$ muodostamisessa ei tarvitse käydä läpi kuin ainoastaan samat solmut $v_{i-1}, v_{i-2}, ...,v_{j-1}$, joille luotiin uudet lapset. Näin ollen on-line algoritmin aikavaatimus riippuu ainoastaan puuhun lisättävien uusien solmujen lukumäärästä, jolloin kokonaisaikavaatimukseksi tulee $O(\vert Trie(S)\vert)$.

Normaalin loppuosapuun keskimääräinen koko on $O(n)$, mutta pahimmassa tapauksessa se on neliöllinen. Esimerkki tällaisesta puusta on $Trie(a^nb^na^nb^n)$.