STL Iterators
This section describes STL iterators and introduces central ideas of generic programming.
Iterator Basics
Sequential Search
Consider a simple algorithm find
- Find a particular value in a sequence (linear collection of elements).
- Search from beginning until value is found or end is reached.
As an abstract algorithm this is clear, but can we implement it without specifying what kind of sequence we are dealing with?
Any implementation has to answer the following questions:
- How is the start of the sequence specified?
- How to move forward in the sequence?
- How to recognize the end of the sequence?
- How to access an element of the sequence?
- What is the return value in success?
- What is the return value in failure?
Iterators provide an elegant answer to all these questions.
Iterators
- Iterator is a generalized pointer identifying a position in a container.
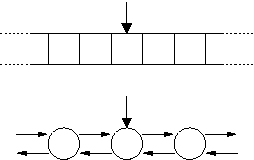
- Allows moving in the container (operator++) and accessing elements (operator*)
Answers to the questions:
- How is the start of the sequence specified?
- iterator to the beginning of the sequence
- How to move forward in the sequence?
- operator++
- How to recognize the end of the sequence?
- iterator to the end of the sequence
- How to access an element of the sequence?
- operator*
- What is the return value in success?
- iterator pointing to the found position
- What is the return value in failure?
- iterator to the end (see below)
Ranges
A range is the standard STL way to specify a sequence. Most STL algorithms take a range as an argument.
- A range is a pair of iterators pointing to the beginning and to the end of the sequence.
- The former points to the first element but the latter to the position one step beyond the last element.
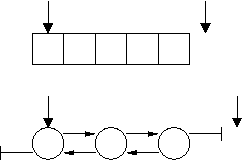
- Range is often denoted as a half-open range [begin,end) or [first,last) or [first,beyond)
- A range [begin,end) is valid if end is reachable from begin by repeated application of operator++.
The asymmetry of begin and end has many nice features:
- [iter,iter) is the empty range.
- The length of [begin,end) is end-begin.
- [A,A+N) is the range for array int A[N];
- end can be used to signal failure of search.
- Loops over all elements are clean:
for (iter = begin; iter != end; ++iter) {
// do something with *iter
}
while (begin != end) {
// do something with *begin
++begin;
}
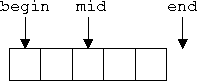
- If mid is in range [begin,end], then
[begin,end) is the concatenation of
[begin,mid) and [mid,end).
- The different choices of mid result exactly the different ways to divide a sequence into two parts.
- When inserting at position iter, the new element is placed just
before the element pointed by iter.
- The resulting sequence is [begin,iter)[new][iter,end).
- Insertion at begin and end work as expected.
Iterators can have three kinds of values:
- A dereferenceable iterator points to an element.
- A past the end iterator points to the one-step-beyond-last position of a container.
- A singular iterator does not point anywhere. It corresponds to null pointers.
The operator* is legal only for dereferenceable iterators.
Algorithm find
We can now give the implementation of the find algorithm.
template <class Iterator, class T>
Iterator find(Iterator begin, Iterator end, const T& value)
{
while (begin != end && *begin != value)
++begin;
return begin;
}
If the returned iterator is end, the value was not found. Otherwise, the iterator points to the value.
This implementation works for any sequence with suitable iterators:
- STL containers (and std::string) have their own iterators:
- vector<int>::iterator, string::iterator
- A container C is [C.begin(),C.end()) as an iterator range.
- Pointers are iterators for primitive arrays.
int A[10]; /* ... */ find (A, A+10, 5);
- input streams
find (istream_iterator<int>(cin), istream_iterator<int>(), 5);
- subrange of a sequence
first = find (begin, end, value); if (first != end) second = find (first+1, end, value);
- customized iterators
- skip elements
- apply a transformation to elements
- ...
Example: Simple List
A very bare-bones singly-linked list can be defined as follows:
struct node {
int val;
node* next;
node (int i, node* n) : val(i), next(n) {}
// implicit copy constructor, copy assignment and destructor
};
We can build a simple list [1, 2, 3] like this
node* list = new node(3,0); list = new node(2, list); list = new node(1, list);
Now define an iterator for the list.
struct node {
// as before
struct iterator {
node* ptr;
iterator (node* p = 0) : ptr(p) {}
// implicit copy constructor, copy assignment and destructor
int& operator* () { return ptr->val; }
iterator& operator++ () { ptr = ptr->next; return *this; }
iterator operator++ (int) {
iterator tmp = *this; ++*this; return tmp; }
bool operator== (const iterator& other) const {
return ptr == other.ptr;
}
bool operator!= (const iterator& other) const {
return ptr != other.ptr;
}
};
iterator begin() { return iterator(this); }
iterator end() { return iterator(); }
};
We can now search the list:
node::iterator iter = find (list->begin(), list->end(), 2); assert (*iter==2);
Note: node::iterator is not quite full STL iterator, yet.
Iterator Categories
The algorithm find uses the following operators of the iterator
- preincrement operator++
- dereference operator*
- comparison operator!=
- copy constructor
The algorithm works for any iterator type that defines the operators properly. Such a list of requirements is sometimes called a concept.
Concepts
A concept is a set of requirements on a type:
- Syntactic requirements state the expressions that should be legal.
- Semantic requirements state what the effects of the expressions should be.
A full description of the requirements can be complicated, especially for semantic requirements. It is often more intuitive to think concepts in terms of related algorithms and types:
- Algorithms that make no assumptions about the type of their
template argument except that it satisfies the requirements.
- Usually several algorithms.
- Some of the algorithms might have weaker requirements but it may not be worth having a separate concept for them.
- Types that satisfy the requirement. Such a type models the
concept, or is a model of the concept.
- A type can model several concepts.
The models are valid template arguments for the algorithms.
Concepts are central to generic programming. Their role is analogous to virtual base classes in object-oriented programming, with models corresponding to derived classes. An important difference is that concepts are not language structures; they are part of the documentation. One consequence is that built-in types can be models, too.
Analogous to class hierarchies, concepts can form hierarchies, too. If the requirements of a concept A are a superset of the requirements of a concept B:
- A is said to refine B.
- All models of A are also models of B.
Some simple concepts
| Concept | Syntactic requirements |
|---|---|
| Assignable | copy constructor, assignment operator |
| DefaultConstructible | default constructor |
| EqualityComparable | equality and inequality operator |
| LessThanComparable | order comparison with operators <, <=, >=, and > |
A regular type is one that is a model of Assignable, DefaultConstructible, EqualityComparable, and one in which these expressions interact in the expected way. For example, after x = y, we may assume that x == y is true.
Iterator Concepts
STL does not have just one but five iterator concepts
| Concept | Refinement of | Syntactic requirements |
|---|---|---|
| InputIterator | Assignable, EqualityComparable | operator*(), operator->(), operator++(), ... |
| OutputIterator | Assignable | operator*(), operator++() ... |
| ForwardIterator | InputIterator, OutputIterator, DefaultConstructible | ... |
| BidirectionalIterator | ForwardIterator | operator--(), ... |
| RandomAccessIterator | BidirectionalIterator, LessThanComparable | operator+(), operator+=(), operator-(), operator[](), ... |
The hierarchy of iterator concepts looks like this.

These iterator concepts are also called iterator categories. Let us take a closer look at each of them. Full details can be found in the C++ Standard.
Input Iterators
Models
- input stream iterators
copy(istream_iterator<char>(cin), istream_iterator<char>(),
ostream_iterator<int>(cout,"\n"));
- almost all iterators
Algorithms
- find
- copy (source range)
- many others
Syntactic requirements
- operator* (read only)
- operator-> (x->m is same as (*x).m)
- operator++
- operator==, operator!=
- copy constructor, copy assignment
Not required
- writable operator* and operator->
- operator--
- iterator arithmetic (iter+5, iter[5], iter1-iter2)
- order comparisons (iter1 < iter2)
- default constructor
Additionally, input iterators are single pass iterators:
- Only one active iterator position.
- Only an iterator to the active position (active iterator)
can be incremented, which moves the active position.
- For example, p==q does not imply ++p==++q.
- Only an active iterator can be dereferenced.
// begin is active InputIterator p = find(begin, end, val); // p is active (nothing after p has been accessed) InputIterator q = p; // p and q are equal and active ++q; // now only q is active y = *p; // error: p is not active p = find(begin, end, y); // error: begin is not active
This strange restriction is needed to make input stream iterators models of InputIterator.
Output Iterator
Models
- output stream iterators
- insert iterators
list<int> L; front_insert_iterator<list<int> > ii(L); *ii++ = 3; *ii++ = 2; *ii++ = 1; vector<int> V; copy (L.begin(), L.end(), back_inserter(V)); // V = [1,2,3]
- most container iterators
Algorithms
- copy (target range)
- transform (target range)
- many other algorithms that output a sequence
Syntactic requirements
- operator* (write only)
- operator++
- copy constructor, copy assignment
Not required
- readable operator*
- operator->
- operator--
- iterator arithmetic
- any comparisons (even ==)
- default constructor
Output iterators, too, are single pass
- Only one active iterator.
- Each element must be written exactly once.
- Assignments (*iter=val) and increments (++iter) must alternate.
- Prefer expression *iter++ = ....
Output iterator ranges have no end.
- Output streams have no end.
- For example, target range of copy has no end iterator.
- Equality comparisons are not needed.
- Users must make sure that there is enough room.
Forward Iterator
Models
- singly-linked list iterator
- almost all container iterators
Algorithms
- replace
- fill - output iterator ranges have no end
- adjacent_find
template <class ForwardIterator>
ForwardIterator
adjacent_find (ForwardIterator begin, ForwardIterator end) {
if (begin == end) return end;
ForwardIterator next = begin;
while (++next != end) {
if (*begin == *next) return begin;
begin = next;
}
return end;
}
- many others
Syntactic requirements
- same as input iterators and
- writable operator* and operator->
- default constructor
Not required
- operator--
- iterator arithmetic
- order comparisons
Unlike input and output iterators, forward iterators allow both reading and writing. Equally important difference is that forward iterators do not have the single pass restrictions:
- Many active iterators to different positions are allowed.
- An element may be written to many times (not at all).
Models of ForwardIterator can be constant.
- Correspond to pointers to const (const int * p;).
- Attemp to write causes compilation error.
- Standard containers have constant iterators in addition to normal iterators.
- Useful for const correctness.
template <class Container, class T>
bool contains (const Container& C, const T& val) {
Container::const_iterator pos;
// Container::iterator pos; would not compile
pos = find(C.begin(), C.end(), val);
return pos != C.end();
}
Nonconstant iterator types are called mutable. The division to constant and mutable applies to bidirectional and random access iterators, too.
Bidirectional Iterator
Models
- doubly-linked list iterator, for example list<int>::iterator
- many container iterators
Algorithms
- reverse
- inplace_merge
- some others
Syntactic requirements
- same as forward iterator and
- operator--
Not required
- iterator arithmetic
- order comparisons
Random Access Iterator
Models
- pointer to an array
- vector<int>::iterator
- string::iterator
Algorithms
- sort
- many others
Syntactic requirements
- same as bidirectional iterators and
- iterator arithmetic
- order comparisons
Iterator Traits
Value Type
Sometimes a generic algorithm needs to know the value type of its iterator arguments, i.e., the type pointed to by the iterators. For example, to swap the values pointed by two iterators, a temporary variable is needed. (This is not quite how the STL algorithm of the same name is defined):
template <class Iterator>
void iter_swap (Iterator a, Iterator b) {
// define value_type
value_type tmp = *a;
*a = *b;
*b = tmp;
}
But how can the algorithm determine the value type?
- All iterator classes are required to have a member type called value_type.
struct my_iterator {
typedef ... value_type;
...
};
- But pointer are iterators, too. They cannot have a member type.
The solution is a helper template called iterator_traits.
- The basic version works for iterators with the member type:
template <class Iterator>
struct iterator_traits {
typedef typename iterator::value_type value_type;
};
- A partial spezialization takes care of pointer types:
template <class T>
struct iterator_traits<T*> {
typedef T value_type;
};
- There is also a third version for pointers to const to remove the const from the value type.
template <class T>
struct iterator_traits<const T*> {
typedef T value_type;
};
iterator_traits<int*> matches both of the first two versions of the template but the pointer version is chosen by the compiler as more specialized.
Now we can define value_type in iter_swap with this line:
typedef typename iterator_traits<Iterator>::value_type value_type;
Generic algorithms often have typedefs like this in the beginning.
Other associated types
In addition to value_type, iterator_traits define four other types. Such types are often called associated types. Here is what the definition of iterator_traits looks like:
template < class Iterator > struct iterator_traits {
typedef typename Iterator::value_type value_type ;
typedef typename Iterator::difference_type difference_type ;
typedef typename Iterator::pointer pointer ;
typedef typename Iterator::reference reference ;
typedef typename Iterator::iterator_category iterator_category ;
};
template < class T > struct iterator_traits <T* > {
typedef T value_type ;
typedef ptrdiff_t difference_type ;
typedef T* pointer ;
typedef T& reference ;
typedef random_access_iterator_tag iterator_category ;
};
template < class T > struct iterator_traits <const T* > {
typedef T value_type ;
typedef ptrdiff_t difference_type ;
typedef const T* pointer ;
typedef const T& reference ;
typedef random_access_iterator_tag iterator_category ;
};
Difference type
- The type of iterator difference p2 - p1.
- More generally, the type for representing iterator distances and
element counts.
- Defined for all iterators except output iterators.
template <class InputIterator, class T>
typename iterator_traits<InputIterator>::difference_type
count (InputIterator begin, InputIterator end, const T& x) {
typename iterator_traits<InputIterator>::difference_type n = 0;
for ( ; begin != end; ++begin)
if (*begin == x) ++n;
return n;
}
- Usually ptrdiff_t which is standard typedef, usually for
int or long.
- A different type could enable ranges whose size exceeds maximum value of ptrdiff_t.
Pointer and reference
- Return types of operator-> and operator*.
- Usually value_type* and value_type&
- For constant iterators const value_type* and const value_type&
Iterator category
- Identifies the iterator concept modeled by the iterator.
- One of
struct input_iterator_tag {};
struct output_iterator_tag {};
struct forward_iterator_tag : input_iterator_tag {};
struct bidirectional_iterator_tag : forward_iterator_tag {};
struct random_access_iterator_tag : bidirectional_iterator_tag {};
- Used for tag dispatching
Tag Dispatching
Consider an algorithm that moves an iterator n steps forward:
template <class InputIterator, class Distance>
void advance (InputIterator& i, Distance n) {
for ( ; n > 0 ; --n ) ++i;
}
This algorithm works for any iterator except output iterators. (Output iterators must write to every position.). There are two problems, though:
- If n is negative, the iterator is not moved. This is OK for input and forward iterators, but bidirectional iterators should move backwards for negative values:
template <class BidirectionalIterator, class Distance>
void advance (BidirectionalIterator& i, Distance n) {
if (n>=0) for ( ; n > 0 ; --n ) ++i;
else for ( ; n < 0 ; ++n ) --i;
}
- Random access iterators enable a much more efficient implementation:
template <class RandomAccessIterator, class Distance>
void advance (RandomAccessIterator& i, Distance n) {
i += n;
}
Each of the three versions is better than the others in some cases. We would like to have a single advance algorithm that automatically executes the right version based on the iterator category.
- Iterator category can be determined using iterator_traits.
- We cannot just leave it for the compiler, because a compiler knows nothing about iterator categories.
- Runtime dispatching using if or switch does not work, because --i and i += n are illegal expression for some iterators and might not compile.
- We can use compile-time dispatching based on function overloading.
template <class InputIterator, class Distance>
void advance (InputIterator& i, Distance n,
input_iterator_tag) {
for ( ; n > 0 ; --n ) ++i;
}
template <class BidirectionalIterator, class Distance>
void advance (BidirectionalIterator& i, Distance n
bidirectional_iterator_tag) {
if (n<=0) for ( ; n > 0 ; --n ) ++i;
else for ( ; n < 0 ; ++n ) --i;
}
template <class RandomAccessIterator, class Distance>
void advance (RandomAccessIterator& i, Distance n,
random_access_iterator_tag) {
i += n;
}
template <class InputIterator, class Distance>
void advance (InputIterator i, Distance n) {
advance (i, n, typename iterator_traits<Iterator>::iterator_category());
}
Note that forward iterators are directed to the first version, because forward_iterator_tag was derived from input_iterator_tag.
Similar technique is used with the algorithm distance that returns the distance from one iterator to an other:
difference_type size = distance(begin, end);
These algorithms are helpful in writing algorithms that work for even input iterators, but are more efficient for random access iterators.
Defining new iterators
Iterator traits will automatically work for any iterator class that defines the appropriate member types.
- Output iterators may define all except iterator_category to be void.
The easiest way to define the member types is to derive from the standard iterator template.
template < class Category , class Value , class Distance = ptrdiff_t ,
class Pointer = Value*, class Reference = Value&>
struct iterator {
typedef Category category ;
typedef Value value_type ;
typedef Distance difference_type ;
typedef Pointer pointer ;
typedef Reference reference ;
}
For example:
struct my_iterator
: std::iterator<forward_iterator_tag, int>
{
...
}
Example: Simple List (continued)
struct node {
int val;
node* next;
node (int i, node* n) : val(i), next(n) {}
// implicit copy constructor, copy assignment and destructor
// no default constructor
struct iterator
: std::iterator<forward_iterator_tag, int>
{
node* ptr;
explicit iterator (node* p = 0) : ptr(p) {}
// implicit copy constructor, copy assignment and destructor
reference operator* () { return ptr->val; }
iterator& operator++ () { ptr = ptr->next; return *this; }
iterator operator++ (int) {
iterator tmp = *this; ++*this; return tmp; }
bool operator== (const iterator& other) const {
return ptr == other.ptr;
}
bool operator!= (const iterator& other) const {
return ptr != other.ptr;
}
};
struct const_iterator
: std::iterator<forward_iterator_tag, int, ptrdiff_t,
const int*, const int&>
{
const node* ptr;
explicit const_iterator (const node* p = 0) : ptr(p) {}
// implicit copy constructor, copy assignment and destructor
const_iterator (const iterator& i) : ptr(i.ptr) {}
reference operator* () { return ptr->val; }
const_iterator& operator++ () { ptr = ptr->next; return *this; }
const_iterator operator++ (int) {
const_iterator tmp = *this; ++*this; return tmp; }
bool operator== (const const_iterator& other) const {
return ptr == other.ptr;
}
bool operator!= (const const_iterator& other) const {
return ptr != other.ptr;
}
};
friend
bool operator== (iterator a, const_iterator b) {
return a.ptr == b.ptr;
}
friend
bool operator!= (iterator a, const_iterator b) {
return a.ptr != b.ptr;
}
friend
bool operator== (const_iterator a, iterator b) {
return a.ptr == b.ptr;
}
friend
bool operator!= (const_iterator a, iterator b) {
return a.ptr != b.ptr;
}
iterator begin() { return iterator(this); }
iterator end() { return iterator(); }
const_iterator begin() const { return const_iterator(this); }
const_iterator end() const { return const_iterator(); }
};
Iterator Adaptors
The header file iterator declares
- iterator_traits
- iterator
- the tag types
- advance and distance
- some special iterators.
The special iterators, often called iterator adaptors, include:
stream iterators
- istream_iterator
- ostream_iterator
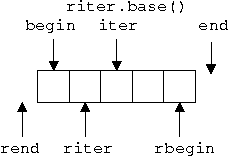
reverse_iterator
- Turns a bidirectional or random access iterator into an iterator moving the opposite direction, but is otherwise just like the original.
- Begin is transformed into end and vice versa.
rbegin = reverse_iterator(end); rend = reverse_iterator(begin);
- Positions are shifted by one due to the asymmetry.
- Member function base() transforms back to the normal iterator.
riter = reverse_iterator(iter); assert (riter.base() == iter);
template <class BidirectionalIterator, class T>
BidirectionalIterator
find_last (BidirectionalIterator begin, BidirectionalIterator end,
const T& value)
{
typedef typename reverse_iterator<BidirectionalIterator> r_iterator;
r_iterator riter = find (r_iterator(end), r_iterator(begin), value);
BidirectionalIterator iter = riter.base();
if (iter == begin) return end;
else return --iter;
}
- Insert iterators and their helper functions
- front_insert_iterator and front_inserter
- back_insert_iterator and back_inserter
- insert_iterator and inserter
- Output iterators for inserting into a container.
list<int> L; front_insert_iterator<list<int> > fii(L); *fii++ = 3; *fii++ = 2; *fii++ = 1; insert_iterator<list<int> > ii(L, L.begin()); *ii++ = 3; *ii++ = 2; *ii++ = 1; vector<int> V; copy (L.begin(), L.end(), back_inserter(V)); // V = [3,2,1,1,2,3]
Example: back_insert_iterator
Let us define the back_insert_iterator as an example.
template <class Container>
class back_insert_iterator
: public std::iterator<output_iterator_tag, void, void, void ,void>
{
private:
Container* container;
public:
typedef Container container_type;
// implicit copy constructor, copy assignment and destructor
// no default constructor
explicit back_insert_iterator(Container& x) : container(&x) {}
back_insert_iterator&
operator=(const typename Container::value_type& value) {
container->push_back(value);
return *this;
}
back_insert_iterator& operator*() { return *this; }
back_insert_iterator& operator++() { return *this; }
back_insert_iterator& operator++(int) { return *this; }
};
The helper function looks like this:
template <class Container>
back_insert_iterator<Container> back_inserter (Container& x) {
return back_insert_iterator<Container>(x);
}
Summary
Generic Programming
- A generic algorithm is a function template that tries to make minimal assumptions about its template arguments.
- The assumptions made are documented as requirements on the argument type.
- A named set of requirements is called a concept.
- A type satisfying the requirements is called a model of the concept.
- Generic algorithms often use advanced template techniques:
- traits
- compile-time dispatching
Iterators
- Iterator is a generalized pointer, a position in a container/sequence.
- Range, a pair of iterators, is the standard way to represent a sequence in STL.
- Most STL algoritms take a range as an argument.
- Five iterator concepts
- input iterator
- output iterator
- forward iterator
- bidirectional iterator
- random access iterator
- Iterator traits are used to determine the associated types.
- Iterator adaptors:
- stream iterators
- reverse iterator
- insert iterators