Introduction
The purpose of this project is to create a compressed version of the 100MB file enwik8, found here. We have implemented a generic Java framework for stream transformations. The framework can be used to convert an input stream into an output stream that contains the coded representation of the input. Both, encoding and decoding, have been implemented as transformating codecs of the framework. We use several algorithms, piped one after another, to gain the results.Burrows-Wheeler Transformation
Burrows-Wheeler transfromation is an encoding, which generates a sequence of repetitive substrings of the given input. The length of the output is slightly longer than the input (a start index is needed for the decosing) but the local density of the characters and short sequences is highly increased.Our implementation is based on the C code that was found from Wikipedia (Burrows-Wheeler transform - Wikipedia). The code has been converted into Java format and the original quick sort was replaced with a merge sort. Implementation of the sort algorithm follows the example that was written by Jason Harrison MergeSortAlgorithm.java.
The input stream is read in blocks and each block (=window) is encoded separately. Length of the window is written into the beginning of the output. Start index of each block follows the actual content. The first implementation was found very slow and the window size was limited to 150KB. Couple of optimizations have been done (worst case check for monotonic sequences and a rolling cache for the compare() function) in order to use 500KB windows.
Move-to-front Transformation
Move-to-front transfortmation is an algorithm that can be used to encode strings. The algorithm replaces each character with its index within a list of possible characters. The character is moved to the first index after the replacement. The transformation is useful for the data compressing algorithms that are dealing with long repetative sequences of various characters as they will be represented with the small indices (the character index will remain zero after the first occurence until another character will push it to the index one). The distribution of indices will be highly bias towards the small numbers and less bits can be used to represent them in comparison to the greater numbers that are less common.Our implementation reads its input in blocks of 30MB. Each block is processed separately and followed by another. The block size (30MB) is stored into the output so that it could be changed without losing the ability to decode the old files.
Arithmetic coding
Our Arithmetic coding is mainly based on the article given to us on the lectures: Witten, Neal, and Cleary, Arithmetic coding for data compression, and on Veli Mäkinen's printed course material: Data Compression Techniques, spring 2006. The main part of the documentation of the Arithmetic coding and the example is from Veli Mäkinen's material (with little modifications according to our implementation).
The basic idea of Arithmetic coding is to map a symbol message into a real interval [a, b) from the base interval, [0,1). Each symbol, s_i, has its own probability p_i and additionally we have a symbol that don't appear anywhere in the message. Each symbol has its own interval, [a_i, b_i), from the base interval, [0, 1) such that, p_i = b_i - a_i. We fix a_1 = 0, b_(n+1) = 1 and a_i < b_i = a_(i+1), where i goes from 1 to n, and a_(i+1) < 1.
The basic encoding goes like:1. Set [a, b) := [0,1)
2. Execute step 3 for each symbol of the message read from left to right
3. [a,b) := [a + (b - a)*a_i , a + (b - a)*b_i)
Example: message 'eoe$' is encoded [0.4082, 0.41):
| initial | [0, 1) |
| reading e: | [0.2 , 0.5) |
| reading o: | [0.38 , 0.44) |
| reading e: | [0.392 , 0.41) |
| reading $: | [0.4082 , 0.41) |
1. Set [a, b) := [0,1)
2. Set x := (c - a)/(b - a). Find i such that a_i = x < b_i. Print symbol s_i.
3. Update the interval according to the symbol: (a, b) := [a + (b - a) *a_i, a + (b - a)*b_i)
4. Repeat step 3 and 4 until i = n+1
While decoding the variable x has values 0.4082, 0.694, 0.47 and 0.9, corresponding to symbols e, o, e and $.
Without the special endsymbol, the decoder would not detect the end of the message. E.g. above [0,0.001] could be any of the message a, aa, aaa, ... (We used the 'stream size' as the mark of the message end.)
This coding practice have serious problem: The encoding of long message requires 'infinite' precision, which we don't have. The solution to this is to use integer arithmetics.
Integer arithmetic usage
The real interval can be set e.g. to an integer interval [0, 2^31). First we find (h in Veli's
pseudocode and the coding interval is [a, b), where a and b are integers) the midpoint, h = 2^30, of the base interval.
Then we start to determing the limits of the coding interval.
The final interval to be encoded is
contained in all intermediate intervals. Each new symbol reveals more and more bits of the prefix of the bit-code of the
final interval. We output the prefix of the code while encoding the symbols. The size of each symbol's own interval
corresponds to the probability to see the symbol in the message. The size, [a_i, b_i), is represented as
count numbers in an array.
We scale the interval according to the symbol at hand.
When encoding starts we use interval [0, 2^31). (In the implementation 0 and Integer.MAX_VALUE , in Java.) After encoding of each symbol
we update the low and high count intervals to be corresponding the current symbol.
The new count values corresponds to the portion of [a_i, b_i)/[a, b) of the currently used
interval. And the portion can be set to correspond the
probability of that symbol, as in the adaptive model - or some else model, even static one. This continues for each symbol.
Briefly same again: The encoder update the interval, when it has seen the symbol and sends
code-bits according to that. The decoder
reads the code and looks for a symbol, which corresponds to the interval,
determined by the code. The initialation must be the same for both and
the update strategy, too. The more same program-code they use the infrequent the
errors in the program-code would be. So the model is usually implemented
for both of them.
The previous is not enough, again we have a problem: It may happen that the midpoint, h, stays
in between a and b during reading many consecutive symbols, and the interval shrinks into
a single integer. The solution to this is to prevent that happenig.
We keep watching that when the 'interval-ends' gets too close to each other,
we scale the interval (for the reason of narrowing too much) again (in addition
to the 'symbol-probability-reason)'.
To implement previous in practice, we devide the initial interval in four equal size
parts, 1/4, 1/4 - 1/2, 1/2 - 3/4 and whole interval. When the interval becomes such that
h/2 <= a < h <= b < 3h/2, we scale the values of a and b into 2*(a - h/2)
and 2*(b - h/2) +1. We keep track of how many scalings
we have done with a counter. When eventually outputting
a bit 0 (or 1), we also print out the counter-value, l, in unary 1^l (or 0^l), and then we zero
the counter. (That means we output as many 0 or 1 as the counter indicates).
After encoding the midpoint is between the beginning and the end of the original interval.
If h - a > b - h we output 01 otherwise 10. This guarantees that we have
output a bit-sequence corresponding to a long enough
prefix identifying an integer inside the message interval.
Decoding is started by reading the code, c, full of bits. Based on those bits,
we can decode the first symbol and the limits a and b.
After this, we call the below 'Decode-pseudocode' like program-code, that fills c so that we can again
decode the next symbol and update the limits a and b, and so on.
Taking into account case h/2 <= a < h <= b < 3h/2 it is enough
to perform as in the else-branch but decrease by h/2 and not by h.
Now the encoding/decoding works correctly unless one of
the probabilities, p_i is too small. (We take care of that in adaptive mode of
our implementation.) More of this adaptation is explained below.
Encode-pseudocode
| while b < h or a >= h do | if b < h then begin | outputbit(0); | a := 2*a; | b := 2*b + 1 end; | else begin | outputbit(1); | a := 2*(a -b) + 1 end; | b := 2*(b -h) + 1 end; |
Decode-pseudocode
| while b < h or a >= h do | if b < h then begin | c := 2*c + inputbit(); | a := 2*a; | b := 2*b + 1 end; | else begin | c := 2*(c - h) + inputbit(); | a := 2*(a -b) + 1 end; | b := 2*(b -h) + 1 end; |
Adaptive model
First we had adaptive model, where the initial probabilities were equal and each symbol had count number set to one (the cumulative count numbers are set according to that). As the coding moved on, the symbols which were seen get larger probability as increasing count-numbers. When the top limit in cumulative counts was reached, all count values were scaled to half of their value. We tried a version where the initial counts were set according to their 'true' distribution, but it didn't make any difference. Also leaving those symbols out which wouldn't be in the input, didn't save any additional space. Because we intended to use more coding methods (Burrows-Wheeler Transformation and Move-to-front Transformation, found elsewere in this report) above Arithmetic coding, we wish to leave the coding as general as possible and wouldn't use this kind of optimization.
In two trial versions of Arithmetic coding there were one version we used end-symbol and on the other the stream ending defined where the coding should stop. Our symbols were 256 byte-values (additionally the end-symbol) with eight bit. The input symbols were read as bytes by the encoder. The decoder read input as bits and decodes (i.e. prints) the symbols according to their byte values. Each symbol had a character representing its byte value. Bytes had only 256 values we used integer values to represent the byte so that the end-symbol could be represented (in the other version). The coding wasn't efficient at this stage 100000000 to 63502180. The encoding-decoding cycle took 10-20 minutes to reach the end. We desided not to use 'end-symbol' alternativity, so, the symbols can be freely used in any encompression stage.
We desided to use implementation of Burrows-Wheeler-type coding and Move-to-front-coding in addition to our Arithmetic coding. We assumed that some kind of Markov model was also needed. So we tried to implement (but we hadn't enough time to complete) a PPM-model (below) to adapt dynamically to the input symbols. The probability counts would again represent the probability of next symbols. And more on, one improvement would have been to adapt the symbol probabilities to a fixed length window and take to account the charcteristic distribution, which the transformations give.
PPM-model
The idea of prediction by partial matching (PPM) is to model the k-th order entropy. Consider a fixed k. We can construct for each k-context of text (charcter sequence with the length k), the distribution of the symbols following the context. Once the text is scanned, the current k-context is known, and the probability of the next symbol can be estimated from the correct distribution. This probability can be encoded using e.g. Arithmetic coding.
PPM uses an adaptive scheme to avoid storing all distributions. Those are constructed on-the-fly while scanning and encoding the text. The problem with adaptive PPM happens when one encounters a new k-context. There is no distribution for the next symbol ready. This can be solved using variable length context:
- If current k-context has not appeared before, then (k - 1)-context is looked for, and so on until a k'-context is found that has appeared before.
- The probability of the next symbol, is then read from the distribution assosiated with the k'-context.
- The decoder has seen the same symbol as the encoder, so it can recognize the same k'-context and decode the same symbol.
- There is a zero-frequency problem when the symbol has not appeared before in the k'-context. An 'escape' symbol is assosiated to each context length. It is encoded if the symbol cannot be encoded in current context. When decoding an escape symbol, the decoder knows to look for the shorter context distribution.
- PPM implementation varies mostly on the heuristics on how assign the escape-symbol probabilities. Updating the context on-the-fly takes time. Encoders are slow, altrough the compression result is much better than with almost any other text compression method.
Stream Transformation Framework
We have implemented a Java application (mam.jar) that can be used for various stream transformations. All encoding have been implemented using this application with a suitable encoder-decoder pair. Our application reads its input from the standard input and writes its output to the standard output stream. The stream based approach allows the free access to all outputs of the subtransformations used within the encoding stack. The whole stack may involve several transformations that have been piped together. Our Wikipedia exercise was encoded using: BWTEnc, M2FEnc, and AriEnc. The meanings of these codecs have been explained below.We have encapsulated our program into an executable jar-file than can be given to the Java virtual machine. The following syntax can be used for generic transformations.
java -jar mam.jar [codec_name] < input_file > output_file
- Currently supported codecs (the list can be obtained by giving no parameters to the program):
- BWTEnc
- Burrows-Wheeler transformation encoder
- BWTDec
- Burrows-Wheeler transformation decoder
- M2FEnc
- Move-to-front transformation encoder
- M2FDec
- Move-to-front transformation decoder
- AriEnc
- Arithmetic encoding with an adaptive character distribution model
- AriDec
- Arithmetic decoding with an adaptive character distribution model
- MAMEnc
- Arithmetic encoding with prediction by partial matching
- MAMDec
- Arithmetic decoding with prediction by partial matching
- ZIPEnc
- GNU zip encoder
- ZIPDec
- GNU zip decoder
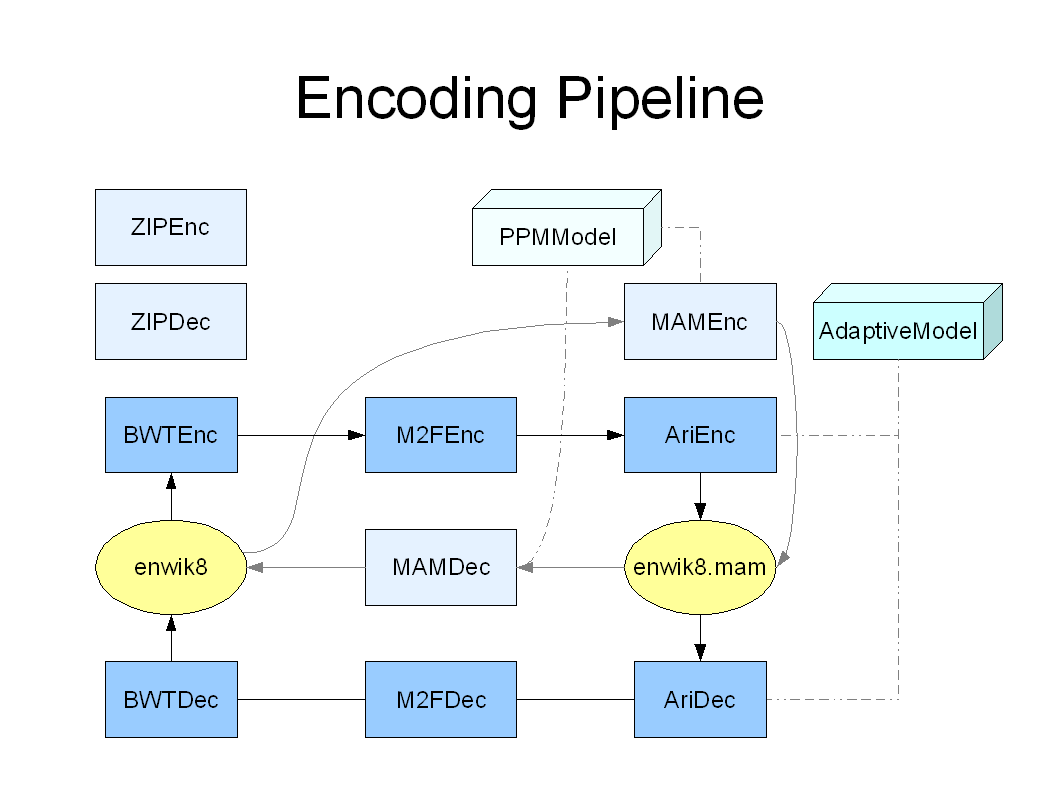
The structure of the our stream transformation framework has been illustrated in Encoding Pipeline image. Blue boxes represent codes that are used in this project and the light cyan boxes represent codes that were used for the testing purposes (ZIP) or were tried to used in this project (MAM). Ari and MAM codecs are based on the same Arithmetic coding module but they have been initialized with their own models. The codecs are connected with arrows that represent the data flow between the components.
Decompressing Wikipedia
MAMDecode is a Linux program that can be used in the computers of Department of computer science. MAMDecode calls our codecs for AriDec, M2FDec, and BWTDec. The decoding takes place in a pipeline, where each codec works in its own thread.
Our encoded file: enwik8.mam (34066116 bytes)The decompression program: MAMDecode (45779 bytes)
Test have been done with dop-1 computer of Department of computer science. It took less than seven minutes to print enwik8 and the memory consumption of the process remained below 60MB. The decoder has been coded so that it takes an advantage of Java threads. The concurrent decoding worked quite well and the Arithmetic coder was able to decode the stream as quickly as it was delivered to it.
Execute in Linux MAMDecode and pipe the encoded file to it with command:
MAMDecode < enwik8.mam > enwik8
We compared our program against Java GZIP by implementing ZIPEnc (GZIP encoder) and ZIPDec (GZIP decoder) codecs using the standard libraries. The adaptive compression works slightly better than GNU zip if it is combined with the Burrows-Wheeler and the move-to-front transformation. The plain Arithmetic encoding produces a file of about 65MB.