


Next: Linear systems
Up: Theory
Previous: Theory
Contents
The theory of dynamical systems is the basic mathematical tool for
analysing time series. This section presents a brief introduction to
the basic concepts. For a more extensive treatment, see for
example [1].
The general form for an autonomous discrete-time dynamical system is
the map
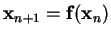 |
(2.1) |
where
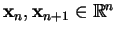 and
and
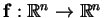 is a diffeomorphism, i.e. a smooth mapping with a smooth
inverse. It is important that the mapping
is a diffeomorphism, i.e. a smooth mapping with a smooth
inverse. It is important that the mapping
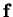 is independent
of time, meaning that it only depends on the argument point
is independent
of time, meaning that it only depends on the argument point
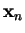 .
Such mappings are often generated by flows of autonomous
differential equations.
.
Such mappings are often generated by flows of autonomous
differential equations.
For a general autonomous differential equation
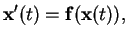 |
(2.2) |
we define the flow by [1]
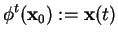 |
(2.3) |
where
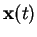 is the unique solution of Equation (2.2)
with the initial condition
is the unique solution of Equation (2.2)
with the initial condition
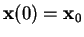 , evaluated at time
, evaluated at time 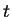 .
The function
.
The function
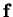 in Equation (2.2) is called the
vector field corresponding to the flow
in Equation (2.2) is called the
vector field corresponding to the flow 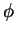 .
.
Setting
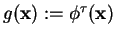 , where
, where 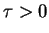 , gives an
autonomous discrete-time dynamical system like in
Equation (2.1). The discrete system defined in this way
samples the values of the continuous system at constant intervals
, gives an
autonomous discrete-time dynamical system like in
Equation (2.1). The discrete system defined in this way
samples the values of the continuous system at constant intervals
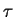 . Thus it is a discretisation of the continuous system.
. Thus it is a discretisation of the continuous system.



Next: Linear systems
Up: Theory
Previous: Theory
Contents
Antti Honkela
2001-05-30
![]() , where
, where ![]() , gives an
autonomous discrete-time dynamical system like in
Equation (2.1). The discrete system defined in this way
samples the values of the continuous system at constant intervals
, gives an
autonomous discrete-time dynamical system like in
Equation (2.1). The discrete system defined in this way
samples the values of the continuous system at constant intervals
![]() . Thus it is a discretisation of the continuous system.
. Thus it is a discretisation of the continuous system.