Junctor & Adjunct
Junctor and Adjunct are programs for Bayesian learning of decomposable graphs from full data. The algorithmic techniques used and some experimental results produced by the programs are presented in the following papers:
K. Kangas, M. Koivisto, and T. Niinimäki. Learning chordal Markov networks by dynamic programming. In Advances in Neural Information Processing Systems 27 (NIPS), 2014.
K. Kangas, T. Niinimäki, and M. Koivisto. Averaging of Decomposable Graphs by Dynamic Programming. In Proceedings of the 31st Annual Conference on Uncertainty in Artificial Intelligence (UAI), 2015.
Decomposable graphs
A decomposable model is an undirected graphical model (Markov network) where the structure graph is decomposable or, equivalently, triangulated, or chordal:
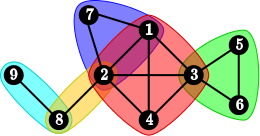
Each decomposable graph can be represented as a junction tree on its cliques, such that for each vertex v the subgraph induced by the cliques containing v is connected:
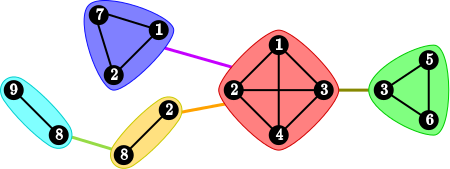
The intersections of adjacent cliques in the tree are called separators.
Learning problem
Our interest is in learning decomposable graphs from known data. In the Bayesian approach we evaluate a model by computing the likelihood, i.e., the probability of the data under that model. For a graph structure the likelihood is obtained by integrating out the the model parameters. From the likelihood we obtain a posterior distribution of decomposable graphs by multiplying with a structure prior and dividing by a normalizing constant.
We wish to find graphs that maximize the posterior probability as well as compute various marginals of the posterior, e.g. the probability of an individual edge. The general problem is NP-hard and the bruteforce method of enumerating all graphs is feasible only up around 8 vertices.
We make use of the fact that, for decomposable graphs, the likelihood factorizes into a product of local components, one term for each clique and separator. This factorization admits dynamic programming over the space of junction trees that makes the learning problem feasible up to around 20 variables.
Given the likelihood (or any similar decomposable score) in terms of local components, we can then perform the following learning tasks:
Finding a maximum-a-posteriori graph
A maximum-a-posteriori graph is a graph that maximizes the posterior probability.
Computing some marginals exactly
Any marginal of the distribution that can be expressed in terms of forbidden cliques or separators can be computed exactly under a uniform prior over rooted junction trees. This includes the absence of a particular edge or a larger pairwise connected subset of vertices. The presence of an edge can be obtained indirectly via complement, and for a larger subsets via inclusion-exclusion.
Estimating marginals via sampling
We can draw independent graph samples from the posterior distribution under the uniform prior of rooted junction trees and thereby obtain a Monte Carlo estimate for any marginal of the distribution. Importance sampling is employed to estimate the marginal under a broader class of priors, such as the uniform prior over decomposable graphs.
Download
The source code (C++11) of the programs is freely available. Compile and usage instructions as well as license details are included in the packages:
Junctor (Junction Trees Optimally Recursively)
Adjunct (Averaging of Decomposable models via Junction Trees)
Adjunct is the most recent version and contains all features of Junctor. It performs the maximization and sampling tasks mentioned above and by default produces estimates of edge probabilities under the uniform prior over decomposable graphs. It also comes with a program DMscore for computing BDeu scores from data.
Junctor is an older version that only finds maximum-a-posteriori graphs.
For any questions regarding the programs, please contact Kustaa Kangas.